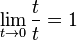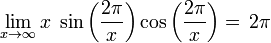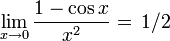François Viète (Fontenay-le-Comte, 1540 - París, 1603). Es considerado uno de los principales precursoeres del álgebra. Empezo a utilizar la geometra como medio para resolver problemas algebraicos, fundando asi lo que el llamo: logistica especiosa, el arte del calculo sobre símbolos.
EL 17 de agosto de 1601 nace Pierre de Fermat, matemático francés que fundó la teoría de números y se anticipó al desarrollo del cálculo diferencial con un método que consistía en estudiar una curva mediante la búsqueda de otras curvas más sencillas que pasaban por arriba y por debajo de la curva bajo estudio.
Newton descubrió el cálculo integral, y luego describió la relación recíproca entre los cálculos diferencial e integral. Sus descubrimientos ocurrieron en Woolsthorpe, aproximadamente en 1665, debido a que Cambridge estaba cerrada como resultado de una epidemia.
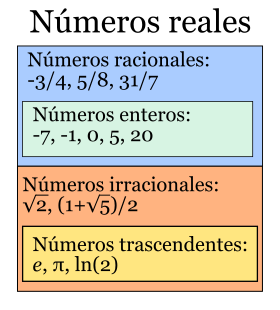
Numeros Reales
En matematicas, los números reales (designados por R) incluyen tanto a los numeros racionales (positivos y negativos y el cero) como a los numeros irracionales (trascendentes, algebraicos), que no se pueden expresar de manera fraccionaria y tienen infinitas cifras decimales no periódicas, tales como:
 .
.Los números reales pueden ser descritos y construidos de varias formas, algunas simples aunque carentes del rigor necesario para los propósitos formales de matemáticas y otras más complejas pero con el rigor necesario para el trabajo matemático formal.
Durante los siglos XVI y XVII el calculo avanzó mucho aunque carecía de una base rigurosa, puesto que en el momento no se consideraba necesario el formalismo de la actualidad, y se usaban expresiones como «pequeño», «límite», «se acerca» sin una definición precisa. Esto llevó a una serie de paradojas y problemas lógicos que hicieron evidente la necesidad de crear una base rigurosa para la matemática, la cual consistió de definiciones formales y rigurosas (aunque ciertamente técnicas) del concepto de número real. En una sección posterior se describirán dos de las definiciones precisas más usuales actualmente: clases de equivalencia de sucesiones de cauchy de números racionales ycortaduras de Dedekind.
Tipos de Numeros Reales
Un número real puede ser un numero racional o un numero irracional. Los números racionales son aquellos que pueden expresarse como el cociente de dos números enteros, tal como 3/4, -21/3, 5, 0, 1/2, mientras que los irracionales son todos los demás. Los números racionales también pueden describirse como aquellos cuya representación decimal es eventualmente periódica, mientras que los irracionales tienen una expansión decimal aperiódica:- Ejemplos
- 1/4 = 0,250000... Es un número racional puesto que es periódico a partir del tercer número decimal.
- 5/7 = 0,7142857142857142857.... Es racional y tiene un período de longitud 6 (repite 714285).
![\frac{\sqrt[3]{7}+1}{2}=1\text{,}456465591386194\ldots](http://upload.wikimedia.org/wikipedia/es/math/f/9/e/f9e0469fdfd9e2047c07e37776ca52da.png) es irracional y su expansión decimal es aperiódica.
es irracional y su expansión decimal es aperiódica.
Otra forma de clasificar los números reales es en algebraicos y trascendentes. Un número es algebraico si existe un polinomio de coeficientes racionales que lo tiene por raíz y es trascendente en caso contrario. Obviamente, todos los números racionales son algebraicos: si
 es un número racional, con p entero y q natural, entonces es raíz del de la ecuación qx=p. Sin embargo, no todos los números algebraicos son racionales.
es un número racional, con p entero y q natural, entonces es raíz del de la ecuación qx=p. Sin embargo, no todos los números algebraicos son racionales.- Ejemplos
- El número
![\frac{\sqrt[3]{7}+1}{2}](http://upload.wikimedia.org/wikipedia/es/math/2/0/a/20adde2b96dd019de6c9bf35f73f85f4.png) es algebraico puesto que es la raíz del polinomio
es algebraico puesto que es la raíz del polinomio 
- Un ejemplo de número trascendente es


Sistema de Coordenadas
Un sistema de coordenadas es un sistema que utiliza uno o más números (coordenadas) para determinar unívocamente la posición de un punto o de otro objeto geométrico. El orden en que se escriben las coordenadas es significativo y a veces se las identifica por su posición en una tupla ordenada; también se las puede representar con letras, como por ejemplo «la coordenada-x». El estudio de los sistemas de coordenadas es objeto de la geometria analitica, permite formular los problemas geométricos de forma "numérica".
Un ejemplo corriente es el sistema que asigna longitud y latitud para localizar coordenadas . En fisica, un sistema de coordenadas para describir puntos en el espacio recibe el nombre de sistema de referencia.
Tipos de Coordenadas
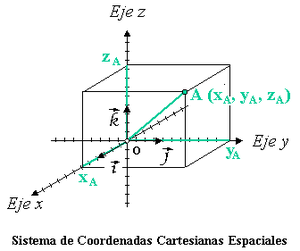
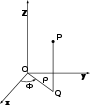
En un espacio euclideo un sistema de coordenadas cartesianas se define por dos o tres ejes ortogonales igualmente escalados, dependiendo de si es un sistema bidimensional o tridimencional (análogamente en  se pueden definir sistemas n-dimensionales). El valor de cada una de las coordenadas de un punto (A) es igual a la proyeccion ortogonal del vector de posición de dicho punto (
se pueden definir sistemas n-dimensionales). El valor de cada una de las coordenadas de un punto (A) es igual a la proyeccion ortogonal del vector de posición de dicho punto ( ) sobre un eje determinado:
) sobre un eje determinado:
 se pueden definir sistemas n-dimensionales). El valor de cada una de las coordenadas de un punto (A) es igual a la proyeccion ortogonal del vector de posición de dicho punto (
se pueden definir sistemas n-dimensionales). El valor de cada una de las coordenadas de un punto (A) es igual a la proyeccion ortogonal del vector de posición de dicho punto ( ) sobre un eje determinado:
) sobre un eje determinado:
Cada uno de los ejes está definido por un vector director y por el origen de coordenadas. Por ejemplo, el eje x está definido por el origen de coordenadas (O) y un versor ( ) tal que:
) tal que:
 ) tal que:
) tal que: , cuyo modulo es
, cuyo modulo es  .
.
Sistema de coordenadas polares
El sistema de coordenadas polares es un sistema de coordenadas bidimensional en el cual cada punto o posición del plano se determina por un angulo y una distancia.
Sistema de coordenadas cilíndricas
El sistema de coordenadas cilíndricas  se usa para representar los puntos de un espacio euclideo tridimensional. Resulta especialmente útil en problemas con simetria axial. Este sistema de coordenadas es una generalización del sistema de coordenadas polares del plano euclídeo, al que se añade un tercer eje de referencia ortogonal a los otros dos. La primera coordenada es la distancia existente entre el eje Z y el punto, la segunda es el ángulo que forman el eje X y la recta que pasa por ambos puntos, mientras que la tercera es la coordenada z que determina la altura del cilindro.
se usa para representar los puntos de un espacio euclideo tridimensional. Resulta especialmente útil en problemas con simetria axial. Este sistema de coordenadas es una generalización del sistema de coordenadas polares del plano euclídeo, al que se añade un tercer eje de referencia ortogonal a los otros dos. La primera coordenada es la distancia existente entre el eje Z y el punto, la segunda es el ángulo que forman el eje X y la recta que pasa por ambos puntos, mientras que la tercera es la coordenada z que determina la altura del cilindro.
 se usa para representar los puntos de un espacio euclideo tridimensional. Resulta especialmente útil en problemas con simetria axial. Este sistema de coordenadas es una generalización del sistema de coordenadas polares del plano euclídeo, al que se añade un tercer eje de referencia ortogonal a los otros dos. La primera coordenada es la distancia existente entre el eje Z y el punto, la segunda es el ángulo que forman el eje X y la recta que pasa por ambos puntos, mientras que la tercera es la coordenada z que determina la altura del cilindro.
se usa para representar los puntos de un espacio euclideo tridimensional. Resulta especialmente útil en problemas con simetria axial. Este sistema de coordenadas es una generalización del sistema de coordenadas polares del plano euclídeo, al que se añade un tercer eje de referencia ortogonal a los otros dos. La primera coordenada es la distancia existente entre el eje Z y el punto, la segunda es el ángulo que forman el eje X y la recta que pasa por ambos puntos, mientras que la tercera es la coordenada z que determina la altura del cilindro.Sistema de coordenadas esféricas
Al igual que las coordenadas cilíndricas, el sistema de coordenadas esféricas se usan en espacios euclídeos tridimensionales. Este sistema de coordenadas esféricas está formado por tres ejes mutuamente ortogonales que se cortan en el origen. La primera coordenada es la distancia entre el origen y el punto, siendo las otras dos los ángulos que es necesario girar para alcanzar la posición del punto.
Coordenadas geográficas
Coordenadas geograficas
Este tipo de coordenadas cartográficas, subtipo de las coordenadas esféricas, se usa para definir puntos sobre una superficie esférica. Hay varios tipos de coordenadas geográficas. El sistema más clásico y conocido es el que emplea la latitud y la longitud, que pueden mostrase en los siguientes formatos:
- DD --- Decimal Degree (Grados Polares): ej. 49.500-123.500
- DM --- Degree:Minute (Grados:Minutos): ej. 49:30.0-123:30.0
- DMS -- Degree:Minute:Second (Grados:Minutos:Segundos): ej. 49:30:00-123:30:00
También se puede definir las coordenadas de un punto de la superficie de la Tierra, utilizando una proyeccion geografica. El sistema de coordenadas cartográficas proyectadas más habitual es el sistema de coordenadas UTM.
Coordenadas curvilíneas generales
Un sistema de coordenadas curvilíneos es la forma más general de parametrizar o etiquetar los puntos de un espacio localmente euclideo o variedad diferenciable (globalmente el espacio puede ser euclídeo pero no necesariamente). Si tenemos un espacio localmente euclídeo M de dimensión m, podemos construir un sistema de coordenadas curvilíneo local en torno a un punto p siempre a partir de cualquier difeomorfismo que cumpla:Para cualquier punto q cercano a p se definen sus coordenadas curvilíneas:
Si el espacio localmente euclídeo tiene la estructura de variedad de Riemann se pueden clasificar a ciertos sistemas de coordenadas curvilíneas en sistema de coordenadas ortogonales y cuando es sistema de coordenadas ortonormales. Las coordenadas colindricas y las coordenadas esfericas son casos particulares de sistemas de coordenadas ortogonales sobre el espacio euclídeo
 .
.Coordenadas curvilíneas ortogonales.
Un sistema de coordenadas curvilíneas se llama ortogonal cuando el tensor metrico expresado en esas coordenadas tiene una forma diagonal. Cuando eso sucede muchas de las fórmulas del cálculo vectorial diferencial se pueden escribir de forma particularmente simple en esas coordenadas, pudiéndose aprovechar ese hecho cuando existe por ejemplo simetria axial, esferica o de otro tipo fácilmente representable en esas coordenadas curvilíneas ortogonales.
Las coordenadas esféricas y cilíndricas son casos particulares de coordenadas curvilíneas ortogonales.
Desigualdades
En matematicas, una desigualdad es una relación que se da entre dos valores cuando estos son distintos (en caso de ser iguales, lo que se tiene es una igualdad).
Si los valores en cuestión son elementos de un conjunto ordenado, como los enteros o los reales, entonces pueden ser comparados.
- La notación a < b significa a es menor que b;
- La notación a > b significa a es mayor que b;
estas relaciones se conocen como desigualdades estrictas, puesto que a no puede ser igual a b; también puede leerse como "estrictamente menor que" o "estrictamente mayor que".
- La notación a ≤ b significa a es menor o igual que b;
- La notación a ≥ b significa a es mayor o igual que b;
estos tipos de desigualdades reciben el nombre de desigualdades amplias (o no estrictas).
- La notación a ≪ b significa a es mucho menor que b;
- La notación a ≫ b significa a es mucho mayor que b;
esta relación indica por lo general una diferencia de varios órdenes de magnitud.
La notación a ≠ b significa que a no es igual a b. Tal expresión no indica si uno es mayor que el otro, o siquiera si son comparables.
Tipos de desigualdades
- Transitividad
- Para numeros reales arbitrarios a,b y c:
- Si a > b y b > c entonces a > c.
- Si a < b y b < c entonces a < c.
- Si a > b y b = c entonces a > c.
- Si a < b y b = c entonces a < c.
- Adición y sustracción
- Para numeros reales arbitrarios a,b y c:
- Si a < b entonces a + c < b + c y a − c < b − c.
- Multiplicación y división
- Para números reales arbitrarios a y b, y c diferente de cero:
- Si c es positivo y a < b entonces ac < bc y a/c < b/c.
- Si c es negativo y a < b entonces ac > bc y a/c > b/c.
- Opuesto
- Para números reales arbitrarios a y b:
- Si a < b entonces −a > −b.
- Si a > b entonces −a < −b.
- Recíproco
- Para números reales a y b distintos de cero, ambos positivos o negativos a la vez:
- Si a < b entonces 1/a > 1/b.
- Si a > b entonces 1/a < 1/b.
- Si a y b son de distinto signo:
- Si a < b entonces 1/a < 1/b.
- Si a > b entonces 1/a > 1/b.
Intervalo
Un intervalo (del latin intervallum) es un conjunto comprendido entre dos valores. Específicamente, un intervalo real es un subconjunto conexo de la recta real , es decir, una porción de recta entre dos valores dados.
, es decir, una porción de recta entre dos valores dados.
Caracterizticas
El intervalo real es la parte de
es la parte de  que verifica la siguiente propiedad:
que verifica la siguiente propiedad:
Si
 e
e  pertenecen a
pertenecen a  con
con  , entonces para todo
, entonces para todo  tal que
tal que 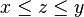 , se tiene que
, se tiene que  pertenece a
pertenece a  .
.
Intervalo abierto
No incluye los extremos.
 o bien
o bien ![]a,b[\](//upload.wikimedia.org/wikipedia/es/math/9/7/d/97d6ce8ff7d3fd1e5118d1e042bfc856.png)
- Notación conjuntista o en términos de desigualdades:

Intervalo cerrado
Sí incluye los extremos.
![[a,b]\](//upload.wikimedia.org/wikipedia/es/math/c/f/c/cfcbcc2c2a41716ab844e25069e87453.png)
- Notación conjuntista o en términos de desigualdades:

Intervalo semiabierto
Incluye únicamente uno de los extremos.
 o bien
o bien  , notación conjuntista:
, notación conjuntista: 
![(a,b]\](//upload.wikimedia.org/wikipedia/es/math/e/1/0/e105896da1efd4783135a0dacd11b9b8.png) o bien
o bien ![]a,b]\](//upload.wikimedia.org/wikipedia/es/math/d/f/1/df16e2650d45bf0cf8f502373865a272.png) , notación conjuntista:
, notación conjuntista: 
- Si a > b, los intervalos descritos no poseen elementos y denotan al conjunto vacio.
- (a,a), [a,a) y (a,a] denotan también al conjunto vacío.
- [a,a] denota al conjunto unitario {a}, también llamado intervalo degenerado.
- Estas notaciones también se utilizan en otras áreas de las matemáticas; por ejemplo, la notación
 , denota un par ordenad en teoria de conjuntos; las coordenadas de un punto o un vector en geometria analitica y algebra lienal; un numero complejo en algebra.
, denota un par ordenad en teoria de conjuntos; las coordenadas de un punto o un vector en geometria analitica y algebra lienal; un numero complejo en algebra. - Ambas notaciones admiten el simbolos
 para indicar que no hay cota.
para indicar que no hay cota.
Ejemplos




Video sobre intervalos
Dominio y contradominio
Dominio: El dominio de es el conjunto de existencia de la misma, es decir, los elementos para los cuales la función está definida. Es el conjunto de todos los objetos que puede transformar, se denota o bien y está definido por:
Recorrido o codominio El recorrido o conjunto de llegada de es el conjunto y se denota o bien
Ejemplos
La función definida por , tiene como dominio e imagen todos los números reales
Función con Dominio X y Codominio YPara la función , en cambio, si bien su dominio es , sólo tendrá como imagen los valores comprendidos entre 0 y +∞ que sean el cuadrado de un número real.
En la figura se puede apreciar una función , con
Note que a cada elemento de X le corresponde un único elemento de Y. Además, el elemento a de Y no tiene origen, y el elemento b tiene dos (el 1 y el 4). Finalmente,
Esta función representada como relación, queda: La función definida por , tiene como dominio e imagen todos los números reales
Función con Dominio X y Codominio YPara la función , en cambio, si bien su dominio es , sólo tendrá como imagen los valores comprendidos entre 0 y +∞ que sean el cuadrado de un número real.
En la figura se puede apreciar una función , con
Note que a cada elemento de X le corresponde un único elemento de Y. Además, el elemento a de Y no tiene origen, y el elemento b tiene dos (el 1 y el 4). Finalmente,
Esta función representada como relación, queda: La función definida por , tiene como dominio e imagen todos los números reales
Función con Dominio X y Codominio YPara la función , en cambio, si bien su dominio es , sólo tendrá como imagen los valores comprendidos entre 0 y +∞ que sean el cuadrado de un número real.
En la figura se puede apreciar una función , con
Note que a cada elemento de X le corresponde un único elemento de Y. Además, el elemento a de Y no tiene origen, y el elemento b tiene dos (el 1 y el 4).
La función definida por , tiene como dominio e imagen todos los números reales
Función con Dominio X y Codominio YPara la función , en cambio, si bien su dominio es , sólo tendrá como imagen los valores comprendidos entre 0 y +∞ que sean el cuadrado de un número real.
En la figura se puede apreciar una función , con
Note que a cada elemento de X le corresponde un único elemento de Y. Además, el elemento a de Y no tiene origen, y el elemento b tiene dos (el 1 y el 4). Finalmente,
Esta función representada como relación, queda: La función definida por , tiene como dominio e imagen todos los números reales
Función con Dominio X y Codominio YPara la función , en cambio, si bien su dominio es , sólo tendrá como imagen los valores comprendidos entre 0 y +∞ que sean el cuadrado de un número real.
En la figura se puede apreciar una función , con
Note que a cada elemento de X le corresponde un único elemento de Y. Además, el elemento a de Y no tiene origen, y el elemento b tiene dos (el 1 y el 4). Finalmente,
Esta función representada como relación, queda: La función definida por , tiene como dominio e imagen todos los números reales
Función con Dominio X y Codominio YPara la función , en cambio, si bien su dominio es , sólo tendrá como imagen los valores comprendidos entre 0 y +∞ que sean el cuadrado de un número real.
En la figura se puede apreciar una función , con
Note que a cada elemento de X le corresponde un único elemento de Y. Además, el elemento a de Y no tiene origen, y el elemento b tiene dos (el 1 y el 4).
Funciones
funciones notacion clasificacion y propiedades
Clasificación de funciones
Funciones algebraicas
En las funciones algebraicas las operaciones que hay que efectuar con la variable independiente son: la adición, sustracción, multiplicación, división, potenciación y radicación.
Las funciones algebraicas pueden ser:
Funciones explícitas
Si se pueden obtener las imágenes de x por simple sustitución.
f(x) = 5x − 2
Funciones implícitas
Si no se pueden obtener las imágenes de x por simple sustitución, sino que es preciso efectuar operaciones.
5x − y − 2 = 0
Funciones polinómicas
Son las funciones que vienen definidas por un polinomio.
f(x) = a0 + a1x + a2x² + a2x³ +··· + anxn
Su dominio es , es decir, cualquier número real tiene imagen.
Funciones constantes
El criterio viene dado por un número real.
f(x)= k
La gráfica es una recta horizontal paralela a al eje de abscisas.
Funciones polinómica de primer grado
f(x) = mx +n
dominio, contradominio, tabulación y graficacion
Uso de una gráfica para determinar el dominio, el contradominio y donde crece o decrece una función
Sea f(x) = 9 –x.
(a) Trazar la gráfica de f.
(b) Determinar el dominio y el contradominio de f.
(c) Determinar los intervalos en los que f sea creciente o decreciente.
Clasificación de funciones
Funciones algebraicas
En las funciones algebraicas las operaciones que hay que efectuar con la variable independiente son: la adición, sustracción, multiplicación, división, potenciación y radicación.
Las funciones algebraicas pueden ser:
Funciones explícitas
Si se pueden obtener las imágenes de x por simple sustitución.
f(x) = 5x − 2
Funciones implícitas
Si no se pueden obtener las imágenes de x por simple sustitución, sino que es preciso efectuar operaciones.
5x − y − 2 = 0
Funciones polinómicas
Son las funciones que vienen definidas por un polinomio.
f(x) = a0 + a1x + a2x² + a2x³ +··· + anxn
Su dominio es , es decir, cualquier número real tiene imagen.
Funciones constantes
El criterio viene dado por un número real.
f(x)= k
La gráfica es una recta horizontal paralela a al eje de abscisas.
Funciones polinómica de primer grado
f(x) = mx +n
dominio, contradominio, tabulación y graficacion
Uso de una gráfica para determinar el dominio, el contradominio y donde crece o decrece una función
Sea f(x) = 9 –x.
(a) Trazar la gráfica de f.
(b) Determinar el dominio y el contradominio de f.
(c) Determinar los intervalos en los que f sea creciente o decreciente.
Operaciones
Una operación es la acción de un operador sobre los elementos de un conjunto. El operador toma los elementos iniciales y los relaciona con otro elemento de un conjunto final que puede ser de la misma naturaleza o no; esto se conoce técnicamente como ley de composición.
El conjunto de partida puede estar formado por elementos de un único tipo (las operaciones aritmeticas actúan sólo sobre números) o de varios (el producto de un vector por un escalar engloba al conjunto unión de vectores y escalares que conforman un espacio vectorial).
Dependiendo de cómo sean los conjuntos implicados en la operación con respecto al conjunto considerado principal según nuestras intenciones podemos clasificar las operaciones en dos tipos: internas y externas.
Tipos de operaciones
Operación interna
Una operación es interna si, tanto los elementos iniciales como los finales pertenecen al único conjunto
es interna si, tanto los elementos iniciales como los finales pertenecen al único conjunto  .
. es un conjunto.
es un conjunto.
- Operaciones finitas si el conjunto inicial
 es producto cartesiano finito.
es producto cartesiano finito.
- Operaciones infinitas en caso contrario.
Operación n-aria.
Diremos que es una operación n-aria en el conjunto
es una operación n-aria en el conjunto  , si:
, si: se le llama la ariedad o anidad.
se le llama la ariedad o anidad.Operación binaria.
Una operación es binaria cuando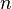 es igual a dos:
es igual a dos:En el conjunto de los numeros naturales,
 , la operación de la adicion:
, la operación de la adicion:  ,
,  , con las diferentes expresiones:
, con las diferentes expresiones:Operación unaria.
Una operación unaria, con un solo parámetro:Ejemplos:
- Dado el conjunto de los números naturales
 , la operación unaria incremento o siguiente, como:
, la operación unaria incremento o siguiente, como:
- Dado el conjunto de los números enteros
 , la operación opuesto, como:
, la operación opuesto, como:
Operación 0-aria
Una operación 0-aria es cuando tenemos una operación es decir:
es decir:- Una operación que designa un elemento distiguido de
 , en teoría de grupos sería el elemento neutro de un grupo.
, en teoría de grupos sería el elemento neutro de un grupo.
Operación externa
Una ley de composición externa sobre un conjunto A con un conjunto B es una aplicación:Ejemplo: Dado el conjunto
 de los vectores en el plano y el conjunto de escalares
de los vectores en el plano y el conjunto de escalares  de números reales, tenemos que el producto de un número real por un vector en el plano es un vector en el plano:
de números reales, tenemos que el producto de un número real por un vector en el plano es un vector en el plano:
Operando
Limite de una funcion
El límite de una función es un concepto fundamental del calculo diferencial matematico, un caso de limite aplicado a las funciones.
Informalmente, el hecho que una función f tiene un límite L en el punto c, significa que el valor de f puede ser tan cercano a L como se desee, tomando puntos suficientemente cercanos a c, independientemente de lo que ocurra en c.
Funciones de variable real
Si la función 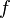 tiene límite
tiene límite  en
en  podemos decir de manera informal que la función
podemos decir de manera informal que la función 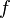 tiende hacia el límite
tiende hacia el límite  cerca de
cerca de  si se puede hacer que
si se puede hacer que  esté tan cerca como queramos de
esté tan cerca como queramos de  haciendo que
haciendo que  esté suficientemente cerca de
esté suficientemente cerca de  siendo
siendo  distinto de
distinto de  .
.
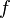 tiene límite
tiene límite  en
en  podemos decir de manera informal que la función
podemos decir de manera informal que la función 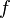 tiende hacia el límite
tiende hacia el límite  cerca de
cerca de  si se puede hacer que
si se puede hacer que  esté tan cerca como queramos de
esté tan cerca como queramos de  haciendo que
haciendo que  esté suficientemente cerca de
esté suficientemente cerca de  siendo
siendo  distinto de
distinto de  .
.
Los conceptos cerca y suficientemente cerca son matemáticamente poco precisos. Por esta razón, se da una definición formal de límite que precisa estos conceptos. Entonces se dice:
El límite de una función f(x), cuando x tiende a c es L si y solo si para todo |
Lo importante es comprender que el formalismo no lo hacen los símbolos matemáticos, sino, la precisión con la que queda definido el concepto de límite. Esta notación es tremendamente poderosa, pues, nos dice que si el límite existe, entonces se puede estar tan cerca de él como se desee. Si no se logra estar lo suficientemente cerca, entonces la elección del δ no era adecuada. La definición asegura que si el límite existe, entonces es posible encontrar tal δ.
No obstante, hay casos como por ejemplo la funcion de Dirichlet  definida como:
definida como:
donde no existe un número c para el cual exista  . Por lo tanto, para demostrar la anterior afirmación es necesario hacer uso del hecho de que cada intervalo contiene tanto numeros racionales como irracionales.
. Por lo tanto, para demostrar la anterior afirmación es necesario hacer uso del hecho de que cada intervalo contiene tanto numeros racionales como irracionales.
 . Por lo tanto, para demostrar la anterior afirmación es necesario hacer uso del hecho de que cada intervalo contiene tanto numeros racionales como irracionales.
. Por lo tanto, para demostrar la anterior afirmación es necesario hacer uso del hecho de que cada intervalo contiene tanto numeros racionales como irracionales.Límites laterales
De manera similar, x puede aproximarse a c tomando valores más grandes que éste (derecha):
Funciones en espacios métricos
Existe otra manera definición de límite que tiene que ver con el concepto de bolas y entornos:
Supóngase f : (M, dM) → (N, dN) es mapeado entre dos espacios metricos, p es un punto limite de M y L∈N. Decimos que "el límite de f en c es L" y escribimosEn términos de desigualdades, tenemos que el límite de la función f(x) en x = c es L si se cumple que para todo ε > 0 existe un δ(ε) > 0 tal que, para todo x:
si
 , entonces
, entonces 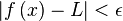
De la desigualdad 0 < | x - c | < δ se obtiene lo siguiente:
- x pertenece a la vecindad ( c - δ , c ) U ( c, c + δ ).
- x no es igual a c, pues 0 < | x - c | implica x distinto de c.
- La solución de | f(x) - L | < ε pertenece a intervalo ( L - ε , L + ε ).
Esto proporciona la clave de comprensión del concepto de límite, pues mientras que el valor de x está en la vecindad horizontal alrededor del punto c y agujereada en c con radio delta y centro c, aun cuando en ese punto c no esté definida, el valor de y está en el intervalo vertical con centro en f(c) y radio épsilon.
Propiedades de los límites
Propiedades generales
Si f(x) y g(x) son funciones de variable real y k es un escalar, entonces, se cumplen las siguiente propiedades:| Límite de | Expresión |
|---|---|
| Una constante | 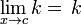 |
| La función identidad | 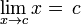 |
| El producto de una función y una constante | 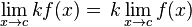 |
| Una suma | 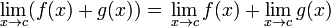 |
| Una resta |  |
| Un producto | 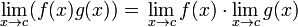 |
| Un cociente | 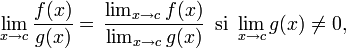 |
| Una potencia |  |
| Un logaritmo |  |
| El numero e |  |
| Función f(x) acotada y g(x) infinitesimal |  . . |
Indeterminaciones
Hay varios tipos de indeterminaciones, entre ellas las siguientes (considere  como el límite que tiende a infinito y
como el límite que tiende a infinito y  al límite cuando tiende a 0; y no al número 0):
al límite cuando tiende a 0; y no al número 0):
 como el límite que tiende a infinito y
como el límite que tiende a infinito y  al límite cuando tiende a 0; y no al número 0):
al límite cuando tiende a 0; y no al número 0):| Operación | Indeterminación |
|---|---|
| Sustracción | 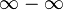 |
| Multiplicación | 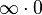 |
| División |  |
| Elevación a potencia | 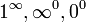 |
- Ejemplo.
Regla de l'Hôpital
Esta regla hace uso de la derivada y tiene un uso condicional. Ésta sólo puede usarse directamente en límites que son «igual» a 0/0 o a ±∞/±∞. Otras formas indeterminadas requieren alguna manipulación algebraica, por lo general, establecer que el límite es igual a y, tomar el logaritmo natural en ambos miembros, y entonces aplicar la Regla de I'Hôpital


 , cuyo modulo es
, cuyo modulo es  .
.





 es la parte de
es la parte de  e
e  pertenecen a
pertenecen a  , entonces para todo
, entonces para todo  tal que
tal que  , se tiene que
, se tiene que  o bien
o bien ![]a,b[\](http://upload.wikimedia.org/wikipedia/es/math/9/7/d/97d6ce8ff7d3fd1e5118d1e042bfc856.png)

![[a,b]\](http://upload.wikimedia.org/wikipedia/es/math/c/f/c/cfcbcc2c2a41716ab844e25069e87453.png)

 o bien
o bien  , notación conjuntista:
, notación conjuntista: 
![(a,b]\](http://upload.wikimedia.org/wikipedia/es/math/e/1/0/e105896da1efd4783135a0dacd11b9b8.png) o bien
o bien ![]a,b]\](http://upload.wikimedia.org/wikipedia/es/math/d/f/1/df16e2650d45bf0cf8f502373865a272.png) , notación conjuntista:
, notación conjuntista: 
 para indicar que no hay cota.
para indicar que no hay cota.


 es un conjunto.
es un conjunto.

 es producto cartesiano finito.
es producto cartesiano finito.









 , la operación opuesto, como:
, la operación opuesto, como:















 existe un
existe un  tal que para todo número real x en el dominio de la función
tal que para todo número real x en el dominio de la función  .
.